24 July 2018 by Sebastian Duchene and Remco Bouckaert
In this post we provide a brief introduction into model adequacy. We describe some theoretical background and the key differences between model adequacy and model selection. This was motivated by the recent release of our BEAST2 package, TreeModelAdequacy, to assess the adequacy of the tree model (sometimes known as the `tree prior') in Bayesian phylogenetic analyses. Model adequacy differs from model selection in that it can assess the absolute, rather than relative, performance of the model. This is useful to assess whether the resulting inferences are reliable and to determine whether key features of the data could have been generated by the model in question. An upcoming post will be a tutorial for using TreeModelAdequacy in a virus data set.
Model selection in phylogenetics
Bayesian phylogenetic methods have increased the range of models for evolutionary analyses. For example, a typical analysis in BEAST2 involves a substitution model, a clock model, and a tree prior, to describe sequence evolution, evolutionary rate variation, and the branching pattern, respectively. We will refer to this ensemble of models as the complete `Bayesian phylogenetic model' (du Plessis and Stadler 2015; Bromham et al. 2018). Model choice is an important aspect of phylogenetic analyses because choosing an incorrect model can lead to misleading inferences.
The impact of the substitution model in estimates of phylogenetic trees was recognised since statistical phylogenetic methods were proposed (Sullivan and Joyce 2005). In general, using an incorrect substitution model can result in incorrect inferences of tree topologies and branch lengths. For this reason, substitution model selection became standard practice in phylogenetic analyses. The typical approach to selecting models consists in considering a pool of models (e.g., a subset of the GTR family) and ranking them with respect to some statistical criteria, such as the Akaike Information Criterion (AIC), the Bayesian Information Criterion (BIC). The AIC and BIC consider the maximum likelihood of the model and penalise the number of parameters to compute a score. Alternatively, models can also be compared based on a likelihood-ratio test, but unlike the AIC and BIC the models being compared must be nested. Popular programs for substitution model selection include JModeltest (Posada 2008). Bayesian approaches to model selection include those based on stepping-stone, path-sampling (Xie et al. 2011; Baele et al. 2013, 2016), and nested-sampling (Maturana et al. 2018). Their aim is to approximate the marginal likelihood of a given model that naturally penalises excess parameters and can be used to effectively select the optimal model.
More recently, there has been a rise in model averaging methods (Posada and Buckley 2004; Baele et al. 2013; Bouckaert and Drummond 2017). The aim of model averaging is to obtain weighted parameter estimates across a range of models. In maximum likelihood this can be done by averaging branch lengths and computing consensus trees over a range of models, using the AIC or BIC scores as weights. In Bayesian phylogenetics, the substitution model can be treated as an unknown `parameter' during the MCMC. The frequency with which models are sampled corresponds to their posterior probability. As such, the best model is that which was most frequently sampled, also known as the Maximum `a posteriori' model (MAP). However, the greatest benefit of model averaging is that it is not necessary to condition the inferences on a single model.
Model adequacy
In spite of the importance of selecting an appropriate model, model selection methods only assess the relative performance of a pool of models. A salient problem about this approach is that it does not assess absolute model performance (Brown and Thomson 2018). Consider a situation where all of the models considered poorly describe the data. Model selection methods will still select one of the models considered, and the researcher will have no information as to whether it captures the main features of the data. In the case of substitution models a common problem is compositional heterogeneity, where very divergent lineages have evolved similar base compositions and most phylogenetic methods may incorrectly cluster them together. Conducting model selection under models of the GTR family only will not reveal that the data are inadequately described by all of these models.
The purpose of model adequacy is to assess whether a given model could have generated the data at hand (Gelman et al. 1996). In practice, this can be done by fitting a model to the data and obtaining estimates for all parameters. These parameter estimates are used to simulate a number of data sets, which represent hypothetical future observations if the model were correct. We consider that a model adequately describes the empirical data if the simulations and empirical data are very similar according to a test statistic. Designing test statistics is a difficult task and is the crux of model adequacy.
Test statistics for model adequacy
There has been substantial work to determine test statistics for substitution models (Huelsenbeck et al. 2001; Bollback 2002; Foster 2004; Ripplinger and Sullivan 2010; Brown 2014; Lewis et al. 2014; Duchêne et al. 2015; Duchene et al. 2016; Duchêne et al. 2018a), with several available implementations (Höhna et al. 2017; Duchêne et al. 2018b). Common test statistics include the multinomial likelihood and a χ2 test of compositional heterogeneity. However, other aspects of the complete Bayesian phylogenetic model have been received less attention, notably those that describe the branching process in phylogenetic trees (Drummond and Suchard 2008), sometimes known as the `tree prior' (du Plessis and Stadler 2015). This is especially relevant in the field of phylodynamics, where a large number of inferences can be drawn from the branching process, such as transmission rates of infectious pathogens (Pybus et al. 2003; Frost and Volz 2010; Stadler et al. 2012). In fact, recently there has been substantial effort in the development of these models to include epidemiological models (Kühnert et al. 2014, 2016; Vaughan et al. 2017), describe population structure (Müller et al. 2017).
We developed TreeModelAdequacy to assess the adequacy of tree models (Duchene et al. 2018a). This package takes a phylogenetic tree as input to infer parameters of the tree model, such as the birth and death rates of a birth-death model. We will refer to this tree as the `empirical tree' and the parameters of the model as η. We estimate the posterior distribution of η. Then we draw a number of random samples, such as 100, from the posterior of η to simulate phylogenetic trees (Fig 1). These phylogenetic trees are known as posterior predictive simulations. Finally, we calculate a number of test statistics for the empirical tree and the posterior predictive simulations. The distribution of a test statistic for the posterior predictive simulations is known as a posterior predictive distribution.
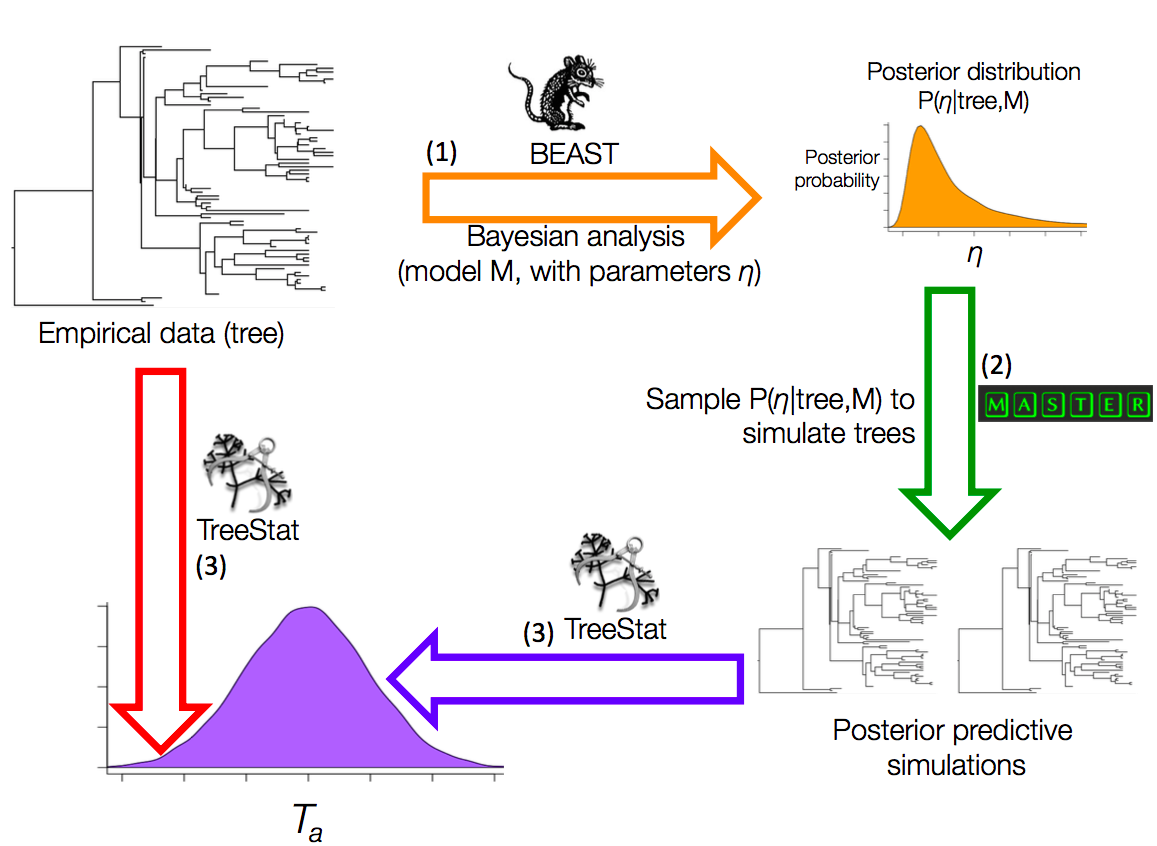 Fig 1. Posterior predictive simulation framework implemented in the TreeModelAdequacy package. Step (1) consists in Bayesian analysis in BEAST under model M to estimate the posterior distribution of parameters η, shown with the arrow and posterior density in orange. In step (2) samples from the posterior are drawn to simulate phylogenetic trees, known as posterior predictive simulations, using MASTER as shown by the green arrow. In step (3) the posterior predictive simulations are analysed in TreeStat to generate the posterior predictive distribution of test statistic Ta, shown by the blue arrow and probability density. Finally, Ta is also computed for the tree from the empirical data using TreeStat, shown by the red arrow, to calculate a posterior predictive probability (pB). Test statistics and pB values can also be computed for trees generated in other programs using TreeModelAdequacyAnalyser, given that the tree from the empirical data and the posterior predictive simulations are provided.
Fig 1. Posterior predictive simulation framework implemented in the TreeModelAdequacy package. Step (1) consists in Bayesian analysis in BEAST under model M to estimate the posterior distribution of parameters η, shown with the arrow and posterior density in orange. In step (2) samples from the posterior are drawn to simulate phylogenetic trees, known as posterior predictive simulations, using MASTER as shown by the green arrow. In step (3) the posterior predictive simulations are analysed in TreeStat to generate the posterior predictive distribution of test statistic Ta, shown by the blue arrow and probability density. Finally, Ta is also computed for the tree from the empirical data using TreeStat, shown by the red arrow, to calculate a posterior predictive probability (pB). Test statistics and pB values can also be computed for trees generated in other programs using TreeModelAdequacyAnalyser, given that the tree from the empirical data and the posterior predictive simulations are provided.
Some examples of test statistics that are informative to assess the tree model are the root-node height, or the ratio of internal to external branch lengths, but there are many more available in TreeModelAdequacy. We determine where the value of the test statistic for the empirical tree falls with respect to the posterior predictive distribution by calculating a posterior predictive p-value for each test statistic, known as pB to distinguish it from the frequentist p-value (Gelman et al. 2014; Duchene et al. 2018a). We consider that a given aspect of the data (e.g., root-node height) is adequately described by the model if pB is between 0.025 and 0.975 (i.e., within the 95% credible interval of the posterior predictive distribution). A basic tutorial for TreeModelAdequacy is available here.
An important aspect of this approach is that it assumes a single tree. The tree can be a summary tree from BEAST or it could be estimated using a different method. If the tree has been estimated using BEAST it is important to verify that it has strong branch support and that the sequence data used to obtain are sufficiently informative (Duchene et al. 2018b). In practice, this can be verified by comparing the prior and posterior distributions.
References
Baele G., Lemey P., Suchard M.A. 2016. Genealogical working distributions for Bayesian model testing with phylogenetic uncertainty. Syst. Biol. 65:250–264.
Baele G., Li W.L.S., Drummond A.J., Suchard M.A., Lemey P. 2013. Accurate model selection of relaxed molecular clocks in bayesian phylogenetics. Mol. Biol. Evol. 30:239–243.
Bollback J.P. 2002. Bayesian model adequacy and choice in phylogenetics. Mol. Biol. Evol. 19:1171–1180.
Bouckaert R., Drummond A.J. 2017. bModelTest: Bayesian phylogenetic site model averaging and model comparison. BMC Evol. Biol. 17:42.
Bromham L., Duchêne S., Hua X., Ritchie A.M., Duchêne D.A., Ho S.Y.W. 2018. Bayesian molecular dating: Opening up the black box. Biol. Rev. 93:1165–1191.
Brown J.M. 2014. Predictive approaches to assessing the fit of evolutionary models. Syst. Biol. 63:289–292.
Brown J.M., Thomson R.C. 2018. Evaluating Model Performance in Evolutionary Biology. Annu. Rev. Ecol. Evol. Syst. In press.
Drummond A.J., Suchard M.A. 2008. Fully Bayesian tests of neutrality using genealogical summary statistics. BMC Genet. 9:68.
Duchêne D.A., Duchêne S., Ho S.Y.W. 2018a. Differences in Performance among Test Statistics for Assessing Phylogenomic Model Adequacy. Genome Biol. Evol. 10:1375–1388.
Duchêne D.A., Duchêne S., Ho S.Y.W., Kelso J. 2018b. PhyloMAd: Efficient assessment of phylogenomic model adequacy. Bioinformatics. 34:2300–2301.
Duchêne D.A., Duchêne S., Holmes E.C., Ho S.Y.W. 2015. Evaluating the adequacy of molecular clock models using posterior predictive simulations. Mol. Biol. Evol. 32.
Duchene S., Bouckaert R., Duchene D.A., Stadler T., Drummond A.J. 2018a. Phylodynamic model adequacy using posterior predictive simulations. Syst. Biol. In press.
Duchene S., Duchene D., Geoghegan J., Dyson Z.A., Hawkey J., Holt K.E. 2018b. Inferring demographic parameters in bacterial genomic data using Bayesian and hybrid phylogenetic methods. BMC Evol. Biol. 18:95.
Duchene S., Di Giallonardo F., Holmes E.C. 2016. Substitution model adequacy and assessing the reliability of estimates of virus evolutionary rates and time scales. Mol. Biol. Evol. 33.
Foster P.G. 2004. Modeling compositional heterogeneity. Syst. Biol. 53:485–495.
Frost S.D.W., Volz E.M. 2010. Viral phylodynamics and the search for an `effective number of infections.' Philos. Trans. R. Soc. London B Biol. Sci. 365:1879–1890.
Gelman A., Carlin J.B., Stern H.S., Dunson D.B., Vehtari A., Rubin D.B. 2014. Model checking. Bayesian data analysis. Boca Raton, Florida: CRC press Boca Raton, FL. p. 141–163.
Gelman A., Meng X.-L., Stern H. 1996. Posterior predictive assessment of model fitness via realized discrepancies. Stat. Sin.:733–760.
Höhna S., Coghill L.M., Mount G.G., Thomson R.C., Brown J.M. 2017. P3: Phylogenetic Posterior Prediction in RevBayes. Mol. Biol. Evol. 35:1028–1034.
Huelsenbeck J.P., Ronquist F., Nielsen R., Bollback J.P. 2001. Bayesian inference of phylogeny and its impact on evolutionary biology. Science. 294:2310–2314.
Kühnert D., Stadler T., Vaughan T.G., Drummond A.J. 2014. Simultaneous reconstruction of evolutionary history and epidemiological dynamics from viral sequences with the birth–death SIR model. J. R. Soc. Interface. 11:20131106.
Kühnert D., Stadler T., Vaughan T.G., Drummond A.J. 2016. Phylodynamics with migration: A computational framework to quantify population structure from genomic data. Mol. Biol. Evol. 33:2102–2116.
Lewis P.O., Xie W., Chen M.-H., Fan Y., Kuo L. 2014. Posterior predictive Bayesian phylogenetic model selection. Syst. Biol. 63:309–321.
Maturana P., Brewer B.J., Klaere S., Bouckaert R. 2018. Model selection and parameter inference in phylogenetics using Nested Sampling. Syst. Biol. In press.
Müller N.F., Rasmussen D.A., Stadler T. 2017. MASCOT: Parameter and state inference under the marginal structured coalescent approximation. Bioinformatics. In press.
du Plessis L., Stadler T. 2015. Getting to the root of epidemic spread with phylodynamic analysis of genomic data. Trends Microbiol. 23:383–386.
Posada D. 2008. jModelTest: Phylogenetic model averaging. Mol. Biol. Evol. 25:1253–1256.
Posada D., Buckley T.R. 2004. Model selection and model averaging in phylogenetics: advantages of Akaike information criterion and Bayesian approaches over likelihood ratio tests. Syst. Biol. 53:793–808.
Pybus O.G., Drummond A.J., Nakano T., Robertson B.H., Rambaut A. 2003. The epidemiology and iatrogenic transmission of hepatitis C virus in Egypt: a Bayesian coalescent approach. Mol. Biol. Evol. 20:381–387.
Ripplinger J., Sullivan J. 2010. Assessment of substitution model adequacy using frequentist and Bayesian methods. Mol. Biol. Evol. 27:2790–2803.
Stadler T., Kouyos R., von Wyl V., Yerly S., Böni J., Bürgisser P., Klimkait T., Joos B., Rieder P., Xie D. 2012. Estimating the basic reproductive number from viral sequence data. Mol. Biol. Evol. 29:347–357.
Sullivan J., Joyce P. 2005. Model selection in phylogenetics. Annu. Rev. Ecol. Evol. Syst. 36:445–466.
Vaughan T.G., Leventhal G.E., Rasmussen D.A., Drummond A.J., Welch D., Stadler T. 2017. Directly Estimating Epidemic Curves From Genomic Data. bioRxiv.:142570.
Xie W., Lewis P.O., Fan Y., Kuo L., Chen M.H. 2011. Improving marginal likelihood estimation for Bayesian phylogenetic model selection. Syst. Biol. 60:150–160.
