1 October 2025 by Remco Bouckaert

Calculating the time bounded probability of a constant population coalescent tree

The bounded coalescent is like the standard coalescent but conditioned on all lineages coalescing before a given time \(t\). An algorithm for calculating the bounded coalescent was introduced in Carson et al, 2022. Unfortunately, its exposition is not clear to me (among other things because it is formulated forward in time), so below you find an alternative description of the algorithm.

Given a tree \(T\) with tips sampled at times \(t_1,\ldots,t_k\), going backward in time and \(t_{k+1}=t\) the maximum time we want to condition on (so \(t_1<t_2<\ldots<t_{k+1}\)). Let \(h(T)\) be the height of the tree \(T\). We assume a constant population \(N\) and want to calculate \(P(T | N, h(T)\le t)\) under a coalescent process. Then \(h(T)>t\) this is zero, but when \(h(T)\le t\) we can calculate \(P(T | N, h(T)\le t)\) as \(P(T | N)/P(h(T)\le t|N)\) where \(P(T|N)\) the standard coalescent probability of \(T\) and \(P(h(T)\le t|N)\) the probability a tree coalesces before time \(t\) (this is Eq(4) in Carson et al, 2022 but with different notation and formulated forward in time). Since we already know how to calculate the standard coalescent in BEAST, what is left is to calculate the conditioning term \(P(h(T)\le t|N)\).

Calculating the conditioning term \(P(h(T)\le t|N)\)

We need to define some terms first

• Let \(L_i\) be the number of tips sampled at time \(t_i\), \(1\le i\le k\).
• Let \(\Delta_i\) be the size of the interval \(t_{i-1}-t_i\), \(1\le i\le k\)
• Let \(p_b(i,j)\) be the probability of having \(j\) lineages just below time \(t_i\) and \(p_a(i,j)\) the same just above time \(t_i\).

Note that the distribution of \(p_a\) is just the distribution of \(p_b\) shifted by the number of lineages sampled at time \(t_i\), so \(p_a(i+L_i,j)=p_b(i,j)\).

So, we start at time \(t_1\), and initialise \(p_a(1,j)\). Since we just sampled \(L_1\) lineages, this means \(p_a(1,j)=1\) for \(j=L_1\) and \(p_a(1,j)=0\) otherwise.

From this we can calculate \(p_b(2,j)\) using Tavaré’s formula for \(g_{i,j}(\Delta t)\) (Eq (6) in Carson et al. 2022), which is the probability of starting at \(i\) lineages and ending in \(j\) \((j\le i)\) lineages after going \(\Delta_t\) backward in time. Here \(\Delta_t=\Delta_1=t_2-t_1\).

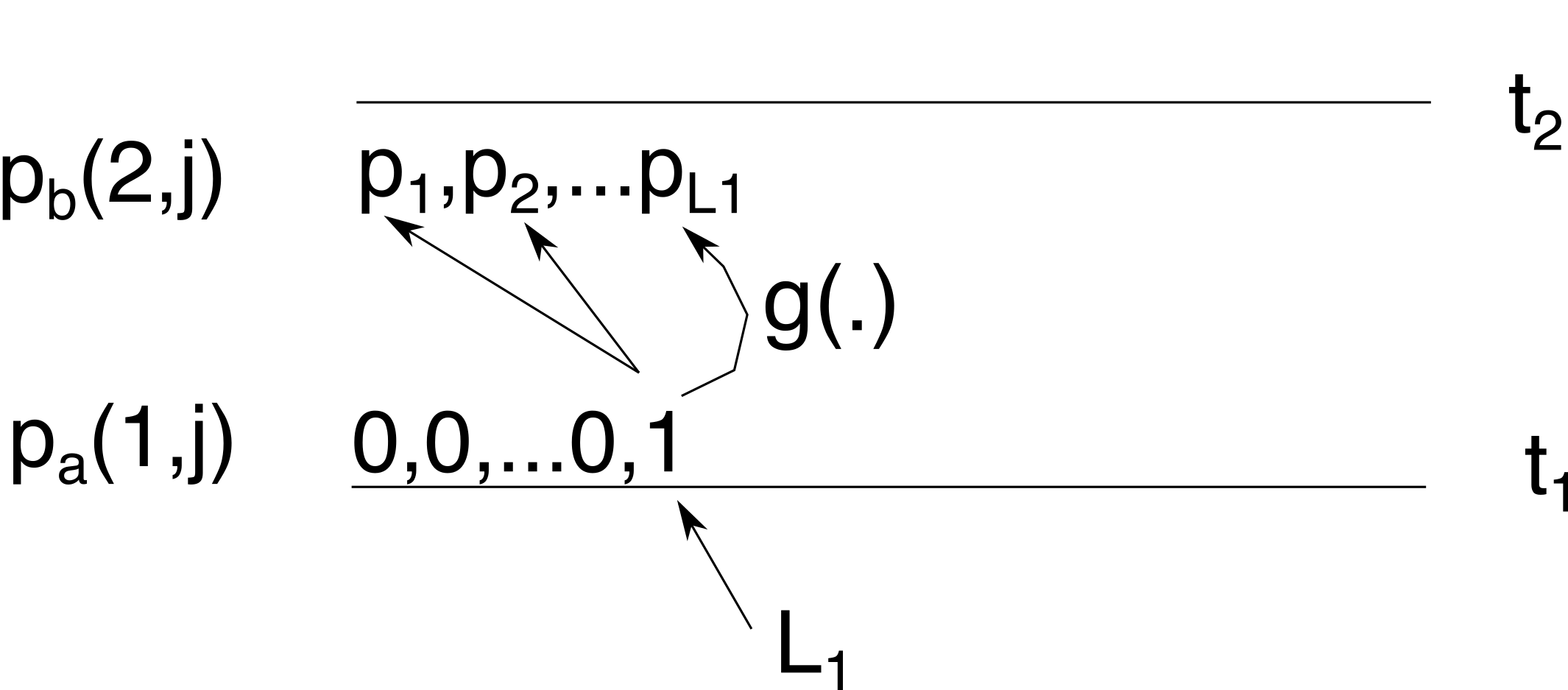
Since we know there is only one non-zero probability at time \(t_1\), we only need to consider going from \(L_1\) lineages to \(1\le j\le L_1\) lineages when reaching time \(t_2\).

At time \(t_2\), we sample \(L_2\) lineages so above time \(t_2\) the distribution \(p_b(2,j)\) shifts with \(L_2\) lineages to give use \(p_a(2,j)\) with \(1\le j\le L_1+L2\):

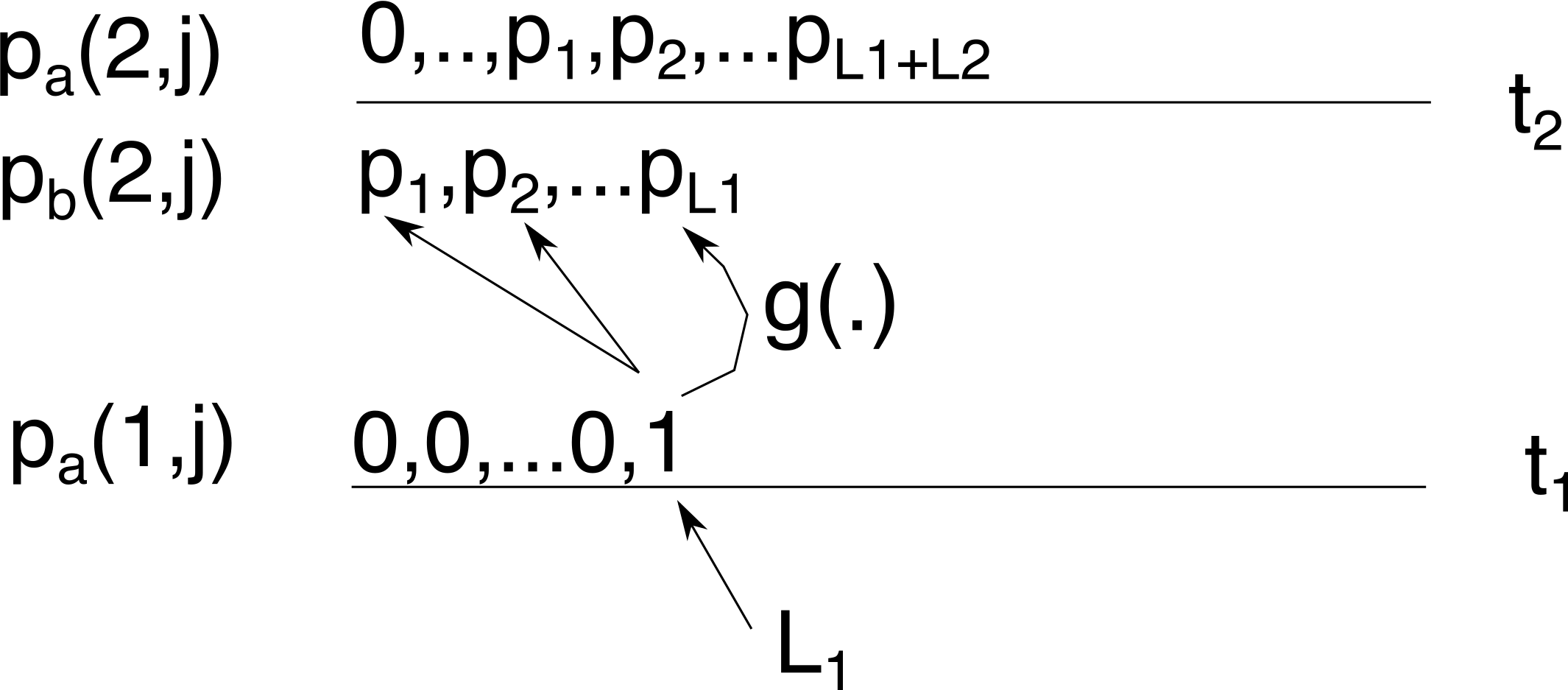
Now, going to time \(t_3\) there is more than one way to obtain 1 lineage: coalescence can start at any of \(L_2\) to \(L_1+L_2\) lineages, and we have to sum them all. Again, we use Tavaré’s \(g_{i,j}(\Delta t)\) function (now with \(\Delta_t=\Delta_2=t_3-t_2\)) and multiply with it with \(p_a(2,j)\) to sum to get \(p_b(3,j)\)

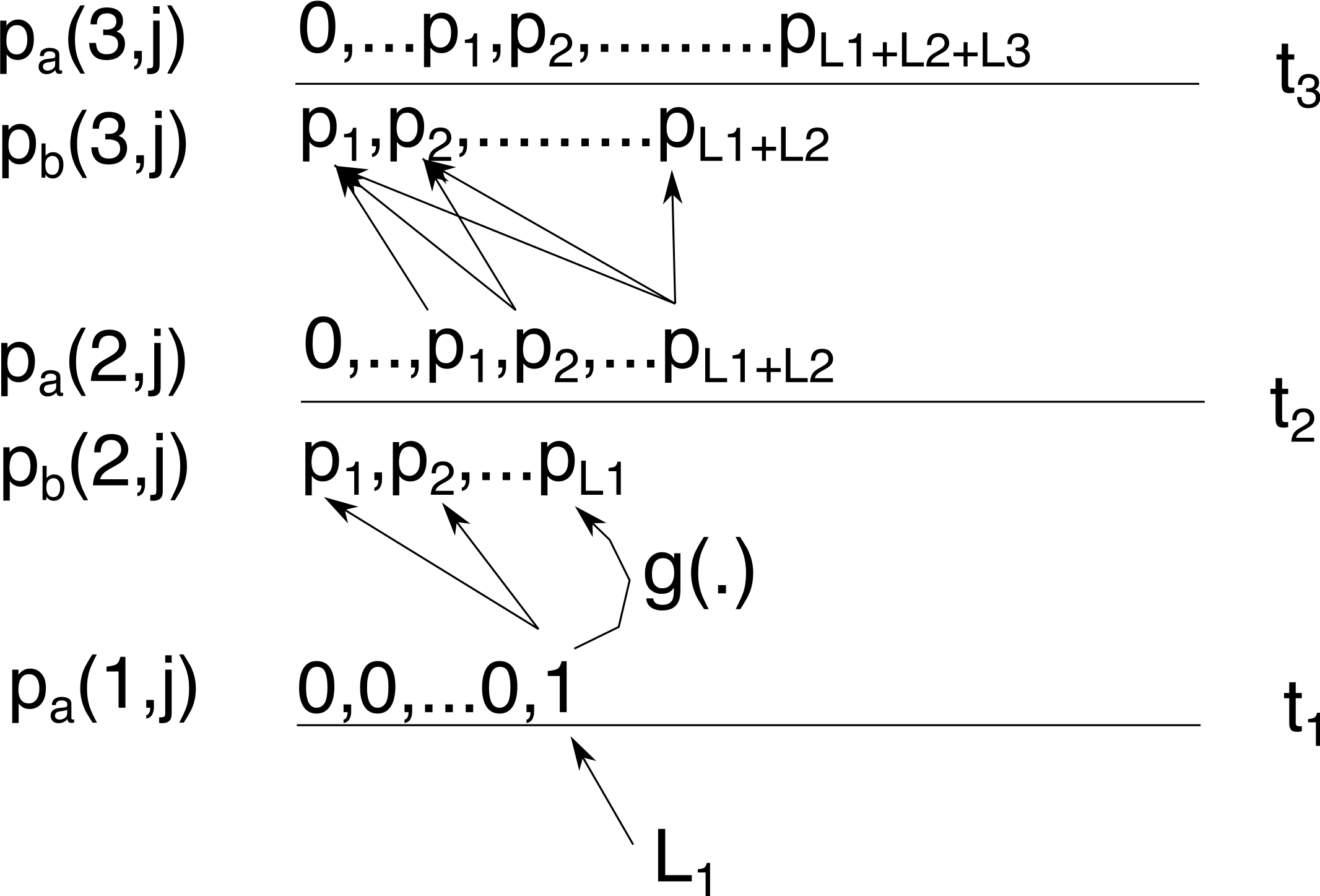
In general \(p_b(i,j) = \sum_{k=j}^{M_i} g_{k,j}(\Delta_i) p_a(i-1,k)\) where \(M_i=\sum_{k=1}^iL_k\).

To get \(p_a(3,j)\) we shift \(p_b(3,j)\) with \(L_3\). We keep repeating till we get to the last sampling time \(t_k\)

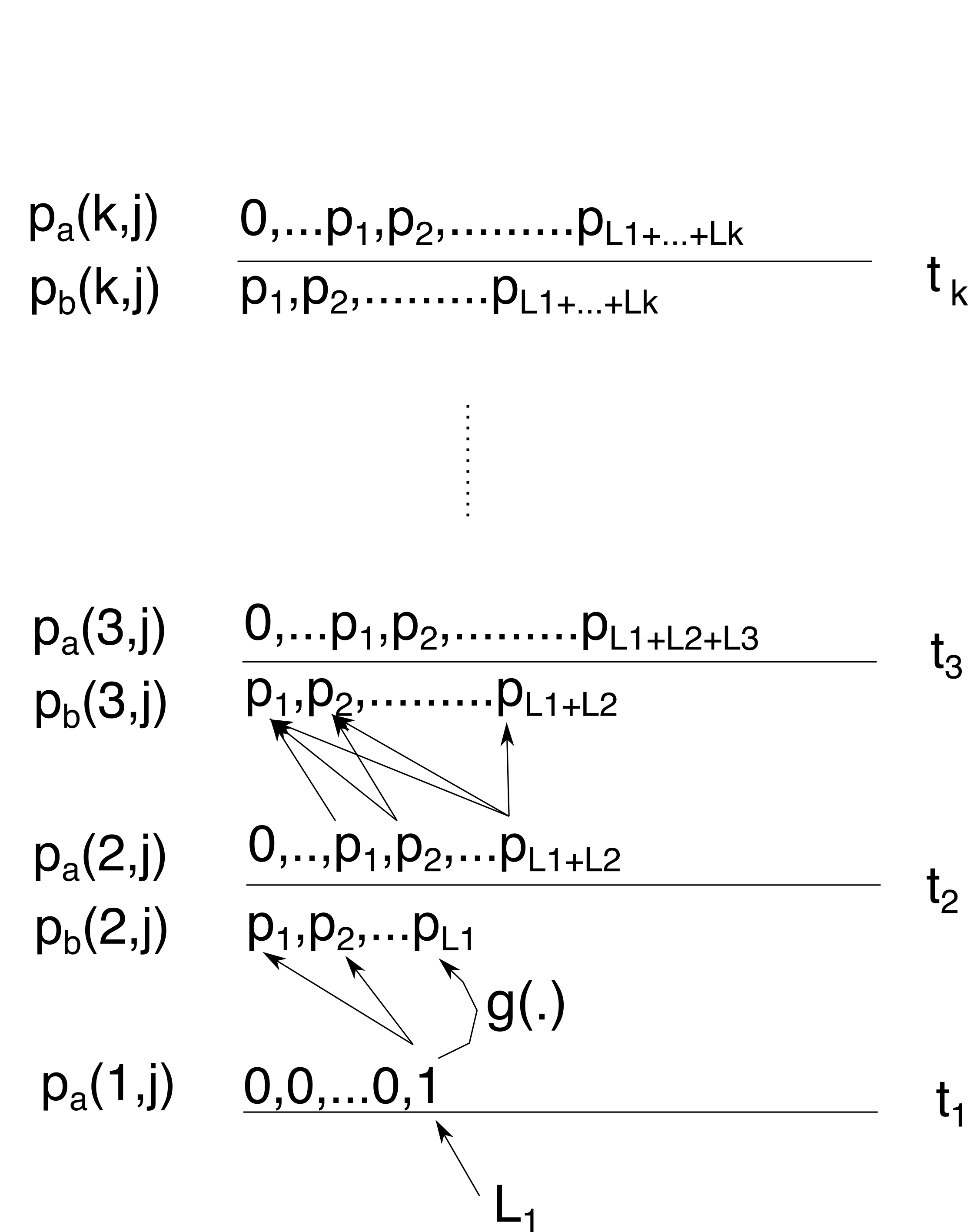
At that point, we can calculate \(p_b(k+1,j)\) for all \(j\), but since we want to know the probability of all lineages having coalesced before time \(t=t_{k+1}\), we only need to calculate \(p_b(k+1,1)\):

And we obtain \(P(h(T)\le t | N)=p_b(k+1,j)\) and are done!

Implementation in BEAST

The algorithm is implemented in the BREATH package as part of the transmission tree likelihood.

References

Carson J, Ledda A, Ferretti L, Keeling M, Didelot X. The bounded coalescent model: conditioning a genealogy on a minimum root date. Journal of Theoretical Biology. 2022 Sep 7;548:111186.

Tavaré S. Line-of-descent and genealogical processes, and their applications in population genetics models. Theoretical population biology. 1984 Oct 1;26(2):119-64.