1 May 2024 by Remco Bouckaert
MCMC is the workhorse of BEAST analyses, however it is limited in the number of taxa it can handle. The main issue is the problematic shape of tree space, which does not allow for a convenient representation in Euclidian space. However, if we are willing to compromise a little by assuming a fixed ordering of taxa, then we can represent all rooted time trees that can be drawn on the particular ordering of taxa. This representation is referred to as a ‘cube’, and it forms a tractable tree distribution that for n taxa represents both topology and node ages by a single point in n-1 dimensional space. The entries in that space can be considered the height of the gap between two consecutive taxa in the ordering.
This idea was recently explored by Bouckaert, 2024, and an algorithme designed to quickly find the cube for various site models and tree priors under a strict clock.
Obviously, not all trees can be represented. For example, for the cube displayed above, the topology of the clade over C, D and E can be ((C,D),E) if h3 is lower than h4 or (C,(D,E)) if h3 is higher than h4, but the topology ((C,E),D) is impossible. This raises the question, how much do we loose by using only a cube to represent the tree posterior. Since not all topologies can be represented any more, are uncertainty estimates still accurate? The answer depends on what we are interested in. The good news is that it passes well calibrated simulation studies (Mendes et al, 2024), and can accurately estimate tree heights and lengths as well as recover site model parameters and hyper paraemters for the tree prior.
However, to establish whether clade support estimates are still accurate, we took all clade support estimates from the well calibrated simulation study and sorted them in bins of associated accuracy. Then, for each of the true trees used to generate the data, for every clade in that tree we looked up the bin that the analysis predicted it would be in. This count determines the height of the bar for the bins. Altogether, we can summarise results in a bar graph, like so.
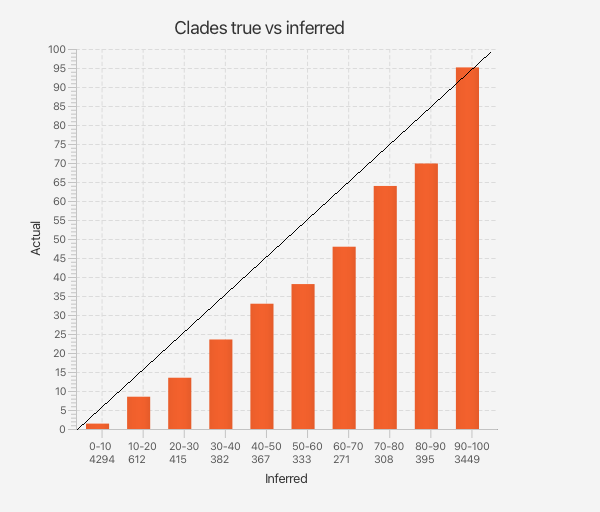
Results for cube space: appart from very small and very large probabilities, clade support tends to be slightly over estimated.
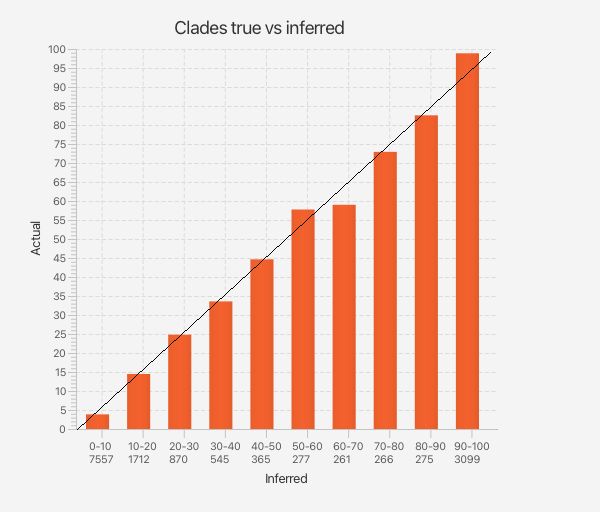
Results for MCMC: most bars end up close to the x=y line, so we conclude that clade support estimates are accurate.
The fact that clade probabilities for cubes are a bit overconfident is no surprise, since not all of tree space is represented, some clades are just not part of the posterior (e.g. like clade CE in the example above). The fact is that it does not seem too far off, making a cube a convenient approximation of posterior distributions. If this can be made to work for a wider range of models, it may be a good compromise between doing a full Bayesian analysis through MCMC, which accurately represents uncertainty, and approximations by a single tree. There are still quite a lot of things that need developing, like support for relaxed clocks, tip dated taxa, etc., but it seems a fruitful way to scale up Bayesian analyses.
References
RR Bouckaert Variational Bayesian Phylogenies through Matrix Representation of Tree Space (bioRxiv, 2023.10. 19.563180) PeerJ 2024
FK Mendes, R Bouckaert, LM Carvalho, AJ Drummond How to validate a Bayesian evolutionary model bioRxiv, 2024.02. 11.579856

